Artificial Neural Network
What is an Artificial Neural Network?
Artificial Neural Network or ANN is a computational model that processes information and allows the system to learn or do things without being explicitly programmed for a task.
The 21st century has brought a lot of drastic changes to humanity, and AI is one of them. AI has taken over many of the industries, and deep learning has played a very vital role in this evolution. Artificial Neural Networks are the building blocks for deep learning; they try to mimic the human brain and help the computer system to learn by examples. These trained systems have now attained accuracy never seen before even surpassing humans. These models are trained by huge data sets that are fed into the neural network architecture consisting of many layers.
The structure of an ANN is inspired by the biological neural system that exists in a human brain. It consists of thousands of small computational units (perceptrons) interlinked together.
These networks are very useful in solving problems that don’t have a defined solution. For example, a well-known use of these networks is to identify the handwritten number. In this case, there are a lot of possibilities, and there is no obvious way to define the handwritten numbers to a computer. Like all the numbers shown below, denote three, but the structure varies for each writing style.
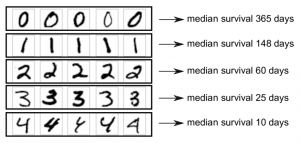
It is mind-blowing how our brains can identify these numbers so effortlessly, but in order to make a computer do this, you need a lot of complex programming.
How does it work?
Artificial Neural Network is not a black box in which you feed information to get the desired results. It is more of a mathematical model whose values are adjusted based on given training data. It consists of many small components that build up to become a complex neural architecture.
The fundamental component of this neural architecture is the perceptron. Perceptron is the small computational units that are linked with one another using the weights. The weights determine the strength of the link between two perceptrons. Each perceptron has a bias that is used to adjust the threshold at which the perceptron will fire/activate.
These perceptrons combine to form layers. In simple cases, the inputs are multiplied with the weights, and bias is added to them. After that, the result is fed into the activation function, which generates the final output of the perceptron.
Basic Math behind ANN
Now let’s discuss the basic computations that are performed in the perceptron. Let us consider a single perceptron that has some inputs, weights, and biases attached to it as shown in the figure below to the right
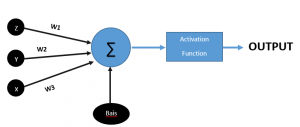
The figure above shows the basic working of the perceptron. X, Y, and Z are the inputs, and W1, W2, and W3 denote the weights. These weights are multiplied by the inputs which give us
z*w1+y*w2+(x*w3)
After that, the bias is added to the equation, and the equation turns into
b+z*w1+y*w2+(x*w3)
This equation is then fed into the activation function, which will generate the output.
Activation Functions and their Types
Activation functions decide the activation state of the perceptron. The output of the perceptron is always a linear function, and after passing it through the activation function, the element of non-linearity is introduced. This non-linearity allows the network to represent any kind of complex function that would not have been possible otherwise. Generally, the activation function of the output layer is different from the one that we use in the hidden layers.
There are mainly three activation functions used in an Artificial Neural Network
- Binary Step Function
This is a threshold-based activation function that gives output in two states, i.e., 0 or 1. The threshold of this function can be adjusted using the bias of the perceptron. The output of this activation function is used as the input for the next layer.

This function is a binary classifier, i.e., it outputs 0 or 1. So, when the number of classes increases i.e., we want output between 0 and 1, this function becomes less effective.
- Sigmoid Activation Function
The sigmoid function is also a mathematical function that limits the output between 0 and 1. Below is the equation for the sigmoid function
fx=11+e-x
The curve of this function is shown bellow
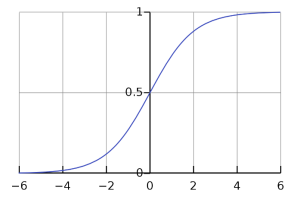
Unlike the binary step function, the output is between 0 and 1, which helps us to predict probability as an output. When a strong negative input is given to this function, it may get stuck, which is the only drawback of this activation function. Other than that, it slows the ANN a bit because the function is a bit complex than other activation functions. And when it is computed thousands of times, a lot of computing power and time is consumed.
- RELU
RELU stands for rectified linear unit, and the mathematical representation of the function is as follows
fx={x for x>0 0 for x<0
The curve of RELU is as follows

It is the most popular and recommended activation function for ANN. It is non-linear in nature and can be combined to approximate any other non-linear function.
How artificial neural network learns?
Multiple layers combine together to form a neural network. There is one input layer, and one output layer, all other layers in between are known as hidden layers. A neural network requires a lot of training data to learn. At first, the data is passed through the input layer, and an output is generated with random weights and biases; this process is known as the forward propagation.
The output of the data is then compared with the actual output, and an error is computed. This error is used to calculate the error function or otherwise known as cost function. This cost function is then analyzed, after which the weights and biases of each layer are adjusted starting from the output layer. This process is known as backward propagation.
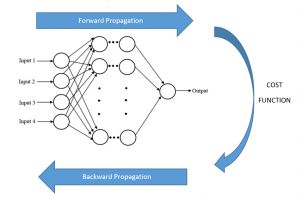
The figure above shows the whole working of the neural network. Remember that making the neural network learns refers to minimizing the cost function by adjusting the weights and biases. In mathematical terms, it refers to finding the minima of the cost function, which can be done through many methods. Batch-Gradient descent and Stochastic-Gradient Descent are the two of the most famous methods used for finding the minima of the cost function.